「マルチプロセッサとプロセス」の版間の差分
編集の要約なし |
|||
| (同じ利用者による、間の4版が非表示) | |||
| 1行目: | 1行目: | ||
=== マルチコアが当たり前の時代に === | |||
以前は(パッケージとしての)CPUの中に1つのプロセッサ(プロセッサ・コア)しか搭載されておらず、それをマザーボードに複数搭載してマルチプロセッサのシステムとして使っていました。 | |||
近年ではデスクトップPCでもノートPCでも採用しているCPUがマルチコアなのが当たり前という時代になってきました。 | |||
マルチコアとは物理的に1つのプロセッサ・チップ (あるいはプロセッサのパッケージの中に) に複数の物理的プロセッサ・コアを搭載しているCPUパッケージのことです。 | |||
部品としてのパッケージ化されたCPUは1つでも、その中には複数のプロセッサが存在しています。 | |||
2018年においては一般に販売されているPCでマルチコア以外はみかけません。 | |||
またスマートフォンやタブレットでもマルチコアのCPUを採用するのが主流となっています。 | |||
=== マルチプロセッサとプロセス === | === マルチプロセッサとプロセス === | ||
| 15行目: | 18行目: | ||
対称マルチプロセッサ(SMP) を構成しているハードウェア上でソフトウェアが対称型マルチプロセッシング(SMP: Symmetric multiprocessing)を実現しています。 | |||
理屈的にはハードウェアがSymmetric Multi-ProcessorでもソフトウェアではSymmetric multiprocessingではないOSの実装もありえます<ref>ありえますが、筆者はそのような実装はみたことはありません。</ref> | |||
が、 | |||
少なくともLinuxのカーネルと、その処理についての文脈でSMPと呼んでいる時、ハードウェアがSMPなものにソフトウェアもSMPを実装しているので結果としておなじ意味になります。 | |||
| 30行目: | 34行目: | ||
ある一定のデータを処理するプログラムをまず仮定します。プロセス単位で割り当てるならプログラム側はSMPを何にも意識しなくても構いません。たくさんのプロセスがスケジュールされている場合でもCPU が多い分、自分の番が回ってくる回数が増えるため負荷に強いという意味で、処理能力が向上します。CPUが1個の時に同時に2つのプロセスを動かす時の処理時間とCPUが2個の時に同時に2つのプロセスを動かす時の処理時間を比較すると、後者の方が速くなります。しかし1つのプロセスに着目してみればCPUが1個で1つのプロセスしか動いていない時の処理時間よりは速くなることがありません。 | ある一定のデータを処理するプログラムをまず仮定します。プロセス単位で割り当てるならプログラム側はSMPを何にも意識しなくても構いません。たくさんのプロセスがスケジュールされている場合でもCPU が多い分、自分の番が回ってくる回数が増えるため負荷に強いという意味で、処理能力が向上します。CPUが1個の時に同時に2つのプロセスを動かす時の処理時間とCPUが2個の時に同時に2つのプロセスを動かす時の処理時間を比較すると、後者の方が速くなります。しかし1つのプロセスに着目してみればCPUが1個で1つのプロセスしか動いていない時の処理時間よりは速くなることがありません。 | ||
=== マルチプロセッサとスレッド === | === マルチプロセッサとスレッド === | ||
2021年10月8日 (金) 18:57時点における最新版
マルチコアが当たり前の時代に
以前は(パッケージとしての)CPUの中に1つのプロセッサ(プロセッサ・コア)しか搭載されておらず、それをマザーボードに複数搭載してマルチプロセッサのシステムとして使っていました。 近年ではデスクトップPCでもノートPCでも採用しているCPUがマルチコアなのが当たり前という時代になってきました。 マルチコアとは物理的に1つのプロセッサ・チップ (あるいはプロセッサのパッケージの中に) に複数の物理的プロセッサ・コアを搭載しているCPUパッケージのことです。 部品としてのパッケージ化されたCPUは1つでも、その中には複数のプロセッサが存在しています。 2018年においては一般に販売されているPCでマルチコア以外はみかけません。 またスマートフォンやタブレットでもマルチコアのCPUを採用するのが主流となっています。
マルチプロセッサとプロセス
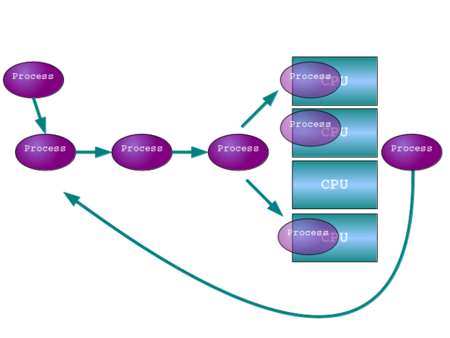
複数のプロセッサの話題に移りますが、ここでの複数プロセッサといってもスーパーコンピュータのように超並列とかは、この話題の範囲ではないので除外した上で話を進めます。
さて、我々が現在利用の対象としているタイプのハードウェアは、対称マルチプロセッサ(SMP: Symmetric Multi-Processor) と呼ばれるタイプのものです。SMPの特徴で覚えておかなければならない点は各々のプロセッサが各々独自の入出力を持っていないのと、そして、どのプロセッサもシステム内のすべての構成部分に対して同等にアクセスできることの2点です。
対称マルチプロセッサ(SMP) を構成しているハードウェア上でソフトウェアが対称型マルチプロセッシング(SMP: Symmetric multiprocessing)を実現しています。
理屈的にはハードウェアがSymmetric Multi-ProcessorでもソフトウェアではSymmetric multiprocessingではないOSの実装もありえます[1]
が、
少なくともLinuxのカーネルと、その処理についての文脈でSMPと呼んでいる時、ハードウェアがSMPなものにソフトウェアもSMPを実装しているので結果としておなじ意味になります。
まずはSMPとはプロセッサの数が増えただけで、あとは構成要素を共有していると理解するのが良いでしょう。ですからSMPの良い部分は単一プロセッサと同じプログラムのモデルが使用できる点です。考えた方として単純にプロセッサが複数あると考えて構いません。単純化したスケジュールのモデルで考えてみましょう。たとえばラウンドロビンのスケジュールを用いて、CPU(ここでの説明はプロセッサと同じということで捉えてください)が1つだったのを2つにしたときを考えてみると下のようになります。
カーネルがSMPの複数CPUに対し処理を割り当てる方法はいくつかあります。それはプロセス単位での割り当てとスレッド単位の割り当てです。
- 補足
- ここではプロセス (1タスク/1スレッド) と タスク ( 1タスク / 複数スレッド ) とし、前者が「プロセス単位で」、後者が「スレッド単位」でという意味です。
ある一定のデータを処理するプログラムをまず仮定します。プロセス単位で割り当てるならプログラム側はSMPを何にも意識しなくても構いません。たくさんのプロセスがスケジュールされている場合でもCPU が多い分、自分の番が回ってくる回数が増えるため負荷に強いという意味で、処理能力が向上します。CPUが1個の時に同時に2つのプロセスを動かす時の処理時間とCPUが2個の時に同時に2つのプロセスを動かす時の処理時間を比較すると、後者の方が速くなります。しかし1つのプロセスに着目してみればCPUが1個で1つのプロセスしか動いていない時の処理時間よりは速くなることがありません。
マルチプロセッサとスレッド
スレッド単位で割り当てる場合、実行中プログラムの持つ複数のスレッドが複数のCPUに同時に割り当てられていきます。 その場合はプログラムの処理のスピードは CPU 単体の最大処理速度を越えることが可能になります。 ただ、それでも上手にスレッドを分割し、その処理タイミングをきちんとプログラミングできる場合という前提が満たされることが必要です。
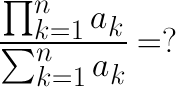
まず、a1 * a2 * a3 * ... * anを計算しAに代入するスレッドとa1 + a2 + a3+ ... + anを計算しBに代入するスレッドを作ります。両方のスレッドの計算の終了を待ってA/Bを計算します。
この時、各々のスレッドが別々のCPUで並列に動くので1個のCPUで全部を計算させるよりも速く計算 [2] ができるはずです。
しかしこの場合、処理効率が単純に2倍に上がるわけではありません。 たとえば1CPUでの計算に20秒かかったとしましょう。 2CPU を使い分母、分子の計算が分割でき並列に計算されたとしても、もし、分子の計算が12秒かかり、分母の計算が10秒かかり、分子÷分母の計算が0.5秒かかったならば、分母の計算時間と割り算の時間を足したものがクリティカルパスですから、その処理時間は12.5秒となります。このようにCPU数が増えたからといって単純に性能がCPU数に合わせて倍数的に増えていくわけではありませんし、もちろん処理が並列化されていないプログラムをいくら走らせても当然ながらその結果はCPUを1つ占有出来ること以上の効果はありません。
- 調べよう
- 並列処理一般において処理効率には上限があることを示しているのがアムダールの法則です。アムダールの法則について調べてみましょう。[3]
脚注
- ↑ ありえますが、筆者はそのような実装はみたことはありません。
- ↑ マルチスレッドを使い円周率を計算したプログラム例: http://uc2.h2np.net/src/mt-bbp.c
- ↑ ジーン・アムダールが書いた1967年の論文 "http://www-inst.eecs.berkeley.edu/~n252/paper/Amdahl.pdf" が公開されています。ここに書かれている並列計算の遅滞に関する内容が後にアムダールの法則と呼ばれるようになります。