「2の補数」の版間の差分
| (同じ利用者による、間の14版が非表示) | |||
| 1行目: | 1行目: | ||
== 2の補数とは == | == 2の補数とは == | ||
2の補数とは2進法を用いて負の値と正の値を表現する際に使われ表現形式です。 | |||
コンピュータの中でNビットの領域を使って正の値と負の値を持った整数を表現する時に使われます。 | |||
最上位ビットを負を意味するサインに使います。 | |||
負の値を示すとき、最上位ビットが1が立っています。 | |||
その時、-2のN乗の値に最上位ビット以外である0からN-2ビット目<ref>0オリジン</ref>までで表している正の整数の値を加えたものが負の整数の値となります。 | |||
表現でNビットを使う整数の、最小値、最大値は以下のようになります。 | |||
| 15行目: | 18行目: | ||
|- | |- | ||
|} | |} | ||
== ワード・バイト・ビットの単位とレジスタ == | == ワード・バイト・ビットの単位とレジスタ == | ||
| 33行目: | 33行目: | ||
{|class="wikitable" | {|class="wikitable" | ||
|+ ビット状態と正10進数との対応 | |||
|- | |||
|4ビットの状態 | |4ビットの状態 | ||
|サインなし | |サインなし | ||
| 92行目: | 94行目: | ||
それ以外のビットは正の値とします。 | それ以外のビットは正の値とします。 | ||
ですので ''1111'' は -8 + 7 = -1 となります。 | ですので ''1111'' は -8 + 7 = -1 となります。 | ||
{|class="wikitable" | 2の補数では次のようになります。 | ||
|+ | |||
10進数表現 | {|class="wikitable sortable" | ||
|+ ビット状態と正負10進数の対応 | |||
!4ビットの状態!!10進数表現 | |||
|- | |- | ||
|0000 | |0000 | ||
| 151行目: | 154行目: | ||
|} | |} | ||
== 2の補数を使っての加算 == | |||
4ビットレジスタで1と-1を加算してみましょう。 | 4ビットレジスタで1と-1を加算してみましょう。 | ||
1はビット表現では0001です。-1はビット表現では1111です。 | 1はビット表現では0001です。-1はビット表現では1111です。 | ||
0001と1111を加算すると2進数では10000です。 | 0001と1111を加算すると2進数では10000です。 | ||
| 218行目: | 163行目: | ||
0000は0です。よって1に-1を加えた結果は0になることがわかります。 | 0000は0です。よって1に-1を加えた結果は0になることがわかります。 | ||
こんどは7に-4を加える計算してみましょう。 | |||
0111と1100を加えると2進数10011となりレジスタの内容は0011となります。 | 0111と1100を加えると2進数10011となりレジスタの内容は0011となります。 | ||
0011は3です。7 + (-4) = 3 ですので同じだといことがわかります。 | 0011は3です。7 + (-4) = 3 ですので同じだといことがわかります。 | ||
== 加算器と2の補数 == | == 加算器と2の補数 == | ||
| 233行目: | 178行目: | ||
* OR どちらかの入力ビットに1があれば1 | * OR どちらかの入力ビットに1があれば1 | ||
* XOR 入力ビットが異なれば1、同じであれば0 | * XOR 入力ビットが異なれば1、同じであれば0 | ||
| 267行目: | 211行目: | ||
では2ビット以上の加算器<ref>暗黙の了承としてビックエンディアンとします。</ref>を考えてみましょう。ここではまず01 + 01 の加算を考えてみます。 | では2ビット以上の加算器<ref>暗黙の了承としてビックエンディアンとします。</ref>を考えてみましょう。ここではまず01 + 01 の加算を考えてみます。 | ||
まず最初のビットは 1 + 1 | まず最初のビットは 1 + 1 です。加算後のビット<ref>加算後の値のことをSumといいます。</ref>は0になります。そして次のビットに1を繰り上げ<ref>繰り上げのことをCarryといいます。</ref>ます。 | ||
この回路のことをHalf | この回路のことをHalf Adderと呼びます。ビット演算回路で示すと下記の「'''Half Adder'''の図」のようになります。 | ||
次のビット以降は下から繰り上がってきたビットも含めて計算することになります。 | 次のビット以降は下から繰り上がってきたビットも含めて計算することになります。 | ||
この回路のことをFull | この回路のことをFull Adderと呼びます。ビット演算回路で示すと下記の「'''Full Adder'''の図」のようになります。 | ||
| 281行目: | 225行目: | ||
|- | |- | ||
|} | |} | ||
=== 4ビット加算器 === | === 4ビット加算器 === | ||
| 296行目: | 238行目: | ||
このように2の補数を使うと加算器で整数(正の値と負の値)を計算することが出来ます。 | |||
== 補足 == | |||
現在は2進数で計算を行うのがあたりまえになっていますが、 | |||
効率的であるかどうかの議論を除けば、計算には3進法でも10進法でも構わなく、過去には[https://en.wikipedia.org/wiki/Ternary_computer 3進法のコンピュータ ]も存在しています。[https://en.wikipedia.org/wiki/Decimal_computer 10進法で計算するコンピュータ]ですが、 | |||
コンピュータ黎明期のマシンとして有名な[https://en.wikipedia.org/wiki/ENIAC ENIAC]は10進数をベースに計算しています。 | |||
ENIACの後継機として設計された[https://en.wikipedia.org/wiki/EDVAC EDVAC]では2進数を採用しています。 | |||
== 脚注 == | |||
2016年5月15日 (日) 18:33時点における最新版
2の補数とは
2の補数とは2進法を用いて負の値と正の値を表現する際に使われ表現形式です。 コンピュータの中でNビットの領域を使って正の値と負の値を持った整数を表現する時に使われます。 最上位ビットを負を意味するサインに使います。 負の値を示すとき、最上位ビットが1が立っています。 その時、-2のN乗の値に最上位ビット以外である0からN-2ビット目[1]までで表している正の整数の値を加えたものが負の整数の値となります。 表現でNビットを使う整数の、最小値、最大値は以下のようになります。
| 最小値 | |
| 最大値 |
ワード・バイト・ビットの単位とレジスタ
CPUとメモリではデータはバイト単位で格納されています。 1か0をあらす最小単位はビットで、8ビットで1バイトになります。 CPU内部で演算をするためのデータを格納している場所は(汎用)レジスタです。 CPUが1回に加算する単位はレジスタのサイズの単位です。そのサイズのことをワードと呼びます。 今日ではワードのサイズには4ビット、8ビット、16ビット、32ビット、64ビットというように2のN乗であるものが主流ですが、12ビットとか18ビットといったものもあります。
4ビットの整数表現を考えてみる
ここで4ビットが1ワードである整数表現を考えてみます。 正の値のみを取る表現だと次のように表現できます。
| 4ビットの状態 | サインなし
10進数表現 |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
ここままでは負の値を表現できません。 そこで2の補数という表現方法を用います。 負の値を表現する時は一番上(最も左のビット)を負を示すサインに使います。 2^3 = 8ですが、それを負の値をみなしますので-8とします。 それ以外のビットは正の値とします。 ですので 1111 は -8 + 7 = -1 となります。
2の補数では次のようになります。
| 4ビットの状態 | 10進数表現 |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | -8 |
| 1001 | -7 |
| 1010 | -6 |
| 1011 | -5 |
| 1100 | -4 |
| 1101 | -3 |
| 1110 | -2 |
| 1111 | -1 |
2の補数を使っての加算
4ビットレジスタで1と-1を加算してみましょう。 1はビット表現では0001です。-1はビット表現では1111です。 0001と1111を加算すると2進数では10000です。 しかし4ビットレジスタなので、5ビット目ははみ出して落ちてしまい0000となります。 0000は0です。よって1に-1を加えた結果は0になることがわかります。
こんどは7に-4を加える計算してみましょう。
0111と1100を加えると2進数10011となりレジスタの内容は0011となります。
0011は3です。7 + (-4) = 3 ですので同じだといことがわかります。
加算器と2の補数
1ビットレジスタの加算器をビット演算を行う回路でどのように表現を考えてみます。 ビット演算 AND、OR、XORを定義します。
- AND 双方の入力ビットが1の時のみ1
- OR どちらかの入力ビットに1があれば1
- XOR 入力ビットが異なれば1、同じであれば0
1ビットだけの加算を考えると次のようになります。
| 0 + 0 = 0 |
| 1 + 0 = 1 |
| 0 + 1 = 1 |
| 1 + 1 = 0 |
1+1が0なのは桁あふれだからです。この加算はXORのビット演算をしているのと同じです。
ですので、1ビットレジスタで加算はXORの回路と同等です(A XOR B → Sの図)。
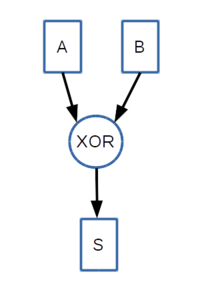 A XOR B → Sの図 |
Half Adder と Full Adder
では2ビット以上の加算器[2]を考えてみましょう。ここではまず01 + 01 の加算を考えてみます。 まず最初のビットは 1 + 1 です。加算後のビット[3]は0になります。そして次のビットに1を繰り上げ[4]ます。 この回路のことをHalf Adderと呼びます。ビット演算回路で示すと下記の「Half Adderの図」のようになります。 次のビット以降は下から繰り上がってきたビットも含めて計算することになります。 この回路のことをFull Adderと呼びます。ビット演算回路で示すと下記の「Full Adderの図」のようになります。
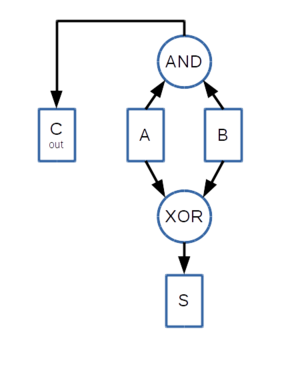 Half Adder の図 |
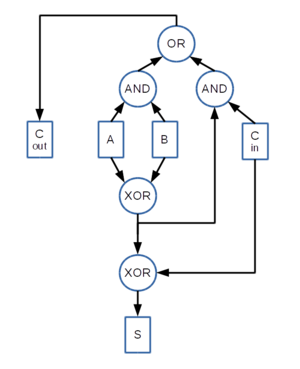 Full Adder の図 |
4ビット加算器
加算器はHalf AdderとFull Adderからなり、4ビット加算器は次のようになります。 最後の繰り上がりビットは無視され、どこにも影響をあたえません。
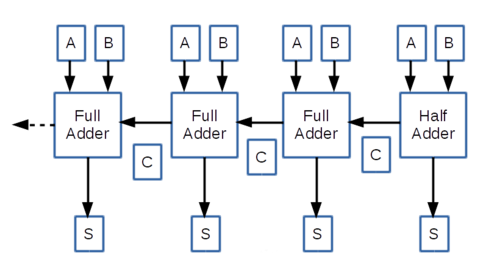 Half AdderとFull Adderを組み合わせ4ビット加算器を作る。 |
このように2の補数を使うと加算器で整数(正の値と負の値)を計算することが出来ます。
補足
現在は2進数で計算を行うのがあたりまえになっていますが、 効率的であるかどうかの議論を除けば、計算には3進法でも10進法でも構わなく、過去には3進法のコンピュータ も存在しています。10進法で計算するコンピュータですが、 コンピュータ黎明期のマシンとして有名なENIACは10進数をベースに計算しています。 ENIACの後継機として設計されたEDVACでは2進数を採用しています。